|
Математический трюк может помочь в лунной навигации
|
| Камилла Цираки, студент-геофизик факультета естественных наук Университета Этвеша Лоранда (ELTE), применила новый подход к исследованию навигационных систем, которые можно использовать на поверхности Луны для планирования будущих путешествий. Работая с профессором Габором Тимаром, главой Департамента геофизики и космических наук, Чираки рассчитал параметры, используемые в земной системе GPS для Луны, используя метод математика Фибоначчи, жившего 800 лет назад. Их результаты были опубликованы в журнале Acta Geodaetica et Geophysica. Сейчас, когда человечество готовится вернуться на Луну спустя полвека, основное внимание уделяется возможным методам лунной навигации. Вполне вероятно, что современным преемникам лунных аппаратов миссий «Аполлон» теперь будет помогать какая-то форма спутниковой навигации, подобная системе GPS на Земле. |
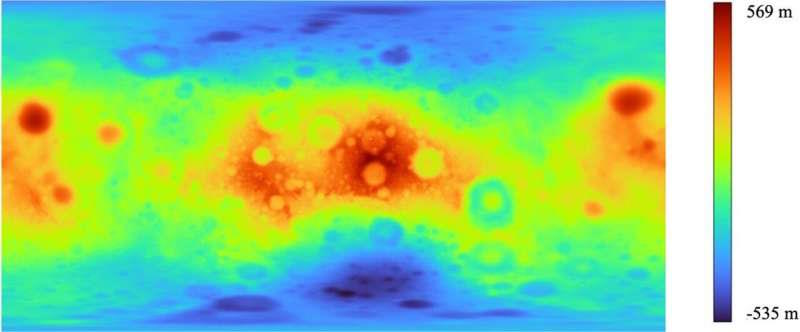
| В случае с Землей эти системы не учитывают реальную форму нашей планеты, геоид, даже не поверхность, определяемую уровнем моря, а вращающийся эллипсоид, который лучше всего соответствует геоиду. Его пересечение представляет собой эллипс, наиболее удаленный от центра масс Земли на экваторе и ближайший к нему на полюсах. Радиус Земли составляет чуть менее 6400 километров, а полюса примерно на 21,5 километра ближе к центру, чем к экватору. Чем интересна форма эллипсоида, которая лучше всего соответствует Луне, и какие параметры можно использовать для ее описания? Почему интересно, что по сравнению со средним радиусом Луны в 1737 километров ее полюса примерно на полкилометра ближе к ее центру масс, чем к экватору? Если мы хотим применить программные решения, опробованные и протестированные в системе GPS, к Луне, нам нужно указать два числа, большую и малую полуоси этого эллипсоида, чтобы программы можно было легко перенести из Земля на Луну. |
|
| Луна вращается медленнее, ее период вращения равен периоду ее обращения вокруг Земли. Это делает Луну более сферической. Это почти сфера, но не совсем. Тем не менее, для картирования Луны, которое было сделано до сих пор, было достаточно приблизить форму сферы, и те, кто больше интересовался формой нашего небесного спутника, использовали более сложные модели. Интересно, что аппроксимация формы Луны вращающимся эллипсоидом никогда раньше не делалась. В последний раз подобные расчеты проводились в 1960-х годах советскими учеными-космонавтами, используя данные со стороны Луны, видимой с Земли. Цираки, студентка второго курса геолого-геофизического факультета, работала со своим научным руководителем Тимаром над расчетом параметров вращающегося эллипсоида, которые лучше всего соответствуют теоретической форме Луны. |
| Для этого они использовали базу данных существующей потенциальной поверхности, называемой лунным селеноидом, из которой они взяли выборку высоты в равномерно расположенных точках на поверхности и искали большую и малую полуоси, которые лучше всего соответствуют вращающейся оси. эллипсоид. Постепенно увеличивая количество точек выборки со 100 до 100 000, значения двух параметров стабилизировались на уровне 10 000 точек. Одним из основных этапов работы было исследование того, как равномерно расположить N точек на сферической поверхности с несколькими возможными решениями; Чираки и Тимар выбрали самую простую, так называемую сферу Фибоначчи. Соответствующая спираль Фибоначчи может быть реализована с помощью очень короткого и интуитивно понятного кода, и основы этого метода были заложены 800-летним математиком Леонардо Фибоначчи. Этот метод также был применен к Земле в качестве проверки, реконструируя хорошее приближение эллипсоида WGS84, используемого GPS. |
| Источник |






